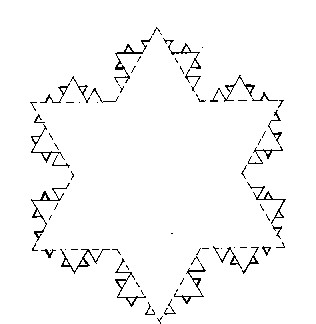
Twentieth Century Upheavals in Science: Relativity and Chaos Theory

1. The general nature of the upheavals

In this chapter we shall look at certain major transformations which violently shook the foundations of science in the first third of the twentieth centuryand which, unlike other already mentioned twentieth century discoveries, made it quite different from previous science. When we examine what happened we can see that a threshold was crossed into something new. In fact, the path followed by the development of science since the seventeenth century, according to the basic principles described in the previous chapter, were gradually to lead it into a very strange world. The world beyond this threshold can teach us a lot from a philosophical point of view and particularly about the possibility of putting soul into science, as will be seen in the later chapters. It is, however, first necessary to understand what happened and for this it is useful to have at least a "taste" of the scientific reasoning involved, which led to the transformation of science. In this part of the book I shall give a fairly non-technical description of the main aspects of the discoveries made and of some of the debates about their significance.

A very important aspect of what was found is that not all things which happen are predictable. This, unlike what was thought previously, is now known to be true even for certain phenomena in the everyday world inhabited by human beings. It is also true in a different rather strange way in the physics of the very small, where what is called quantum physics must be used and, as we shall see, it is even true in mathematics! In addition, the conceptions about the natures of space and time were radically transformed, firstly by the theory of relativity and then more radically by quantum physics, though physics retained its fundamental assumptions based on space and the space-like aspects of time.

Let us start with a major change in scientific ideas, which revolutionized thinking about space and time, but which did not involve the unpredictable. For Newton space was something absolute, separate from the bodies which moved in it and for which his laws of motion were true. Similarly, time was universal in classical physics. It was these ideas which were overthrown by the special and general theories of relativity. There is ambiguity in the classical idea of an absolute space and classical physics in fact contains a sort of "relativity". When no force is acting, bodies can, according to Newton's laws, continue in uniform motion with respect to each other. No one uniform motion is to be preferred to another, as Galileo already knew. If two bodies are moving in the same direction with velocities n ₁ and n ₂, the velocity of one with respect to the other is
n ₂ - n ₁. The length of a rigid rod and the speed of a clock used to measure lengths and intervals of time are then supposed to be constant, as are the velocities derived from the lengths and time intervals.

In a classical framework, it was difficult to understand how light could travel through space. In the nineteenth century space was thought to be filled by a real substance called "ether", in which light waves were thought to travel. In such a situation one might imagine that absolute velocities could be defined and measured with respect to the ether. The earth should then move through it and the effects of such a motion of the earth with respect to the ether should be measurable. Several experiments were made to measure the earth's motion, including in particular those of Michelson in 1881 and of Michelson and Morley in 1887. Because of this motion, light should have taken slightly different times to travel in different directions. No effect was ever seen except in the work of Miller, which is sometimes cited by those who challenge the orthodoxy of present-day physics. His effects are, however, generally considered by physicists to be smaller than the errors.

Though physical effects can be proposed to explain the failure to detect the motion of the earth through the ether, Einstein realized that the reason was something more basic. His special theory of relativity of 1905 applied to bodies moving uniformly with respect to each other. For all such bodies the velocity of light always had to be constant, whereas in Newtonian theory no state of uniform motion was to be preferred to any other. The result of such assumptions is that the measurements of space and time are not the same for two bodies in different places having different speeds. When two bodies are moving with respect to each other, each of the bodies will always appear shortened in the direction of its motion, if seen by an observer moving together with the other body. When its speed relative to the other body equals the speed of light, its observed length approaches zero. In the same way a clock on one of the bodies will appear to the observer moving with the second body to be slower than its own clock. If it was moving with the speed of light relative to the other body, the first clock would appear to be stationary, its time having stopped. The mass of a moving body will also appear to increase when it is measured by an observer moving with another body, becoming infinite when the relative speeds are equal to the speed of light. In fact, special relativity leads to the conclusion that no body can be accelerated beyond the speed of light.

Consideration of the fact that the apparent mass of a body varies with velocity leads to the conclusion that mass and energy are equivalent. The relation is given by Einstein's famous equation

where E is the energy, m the mass and c the speed of light. What is particularly striking is that this equation is also true for the "rest mass" of the body, that is, the mass it appears to have when it is not moving with respect to an observer. This relation is confirmed by experiments and became famous because of its application in the tremendous energy released by nuclear weapons, which convert a significant proportion of their mass into energy.

Special relativity can also be understood geometrically in the framework of the 4 dimensional "space-time" of Minkowski. This can be defined by an observer with respect to whom other observers are moving as containing 3 dimensions of space and one which is derived from the observer's time (time multiplied by the speed of light and by the "imaginary" square root of -1). The path of a particle in this space is called a "world line". "Distances" in this space divided by the speed of light are then equal to the time measured by a clock near a particular particle, moving with it. It would not be easy for such an observer moving with a particle to decide at what time a distant event occurs. One way would be for him to send out a light signal which is immediately reflected if an event occurs far away, the event being in this way detected. The time of the event could be defined as half-way in time between the sending out and the return of the signal. However, another observer would not measure the same time for the event -- even the order in time of two different far away events could be reversed for the two observers. Their experiences in time could be completely different. Minkowski summarized the situation as it appeared to him, by stating that space and time by themselves were doomed to fade away into mere shadows, and only a kind of union of the two would preserve an independent reality. A very clear non-technical description of the apparent paradoxes of special relativity is given in the already mentioned book by Roger Penrose: "The Emperor's New Mind" (pages 191-201).

In 1915 Einstein published an extension of his theory of accelerated motion and gravitation, which is called "general relativity". In this theory space and time are found to be curved. This can be easily be understood if we consider two dimensional analogies. The geometry on the surface of a sphere, for example, will not be the same as that on a flat surface. Straight lines on the flat surface are replaced by parts of great circles on the surface of the sphere which, like straight lines on a flat surface, give the shortest distance between two points. This means that an elastic stretched on the surface of a sphere will lie on a great circle. For a more general surface similar curves are called "geodesics". A gravitational field was found by Einstein to distort space-time and a particle acted on by a gravitational field followed the geodesic. This theory led to a simple explanation of the fact that the mass in Newton's second law of motion can be defined as being the same as that in his law of gravitation (after correcting for the additional effects of relativity).

A number of experimental tests and astronomical observations have confirmed general relativity. For instance, the motion of the planet Mercury can only be fully explained by taking account of general relativity. The planet does not only go round in its orbit, but the elliptical orbit itself also revolves at a rate not predictable by Newton's theory. The bending of light rays passing close to massive objects like the Sun, is also a famous prediction. It is now difficult to challenge general relativity, which is very much used, in particular by those who study the large scale structure of the universe.

However, what must be emphasized is that in spite of the successes of relativity, absolute motion and absolute time have in a certain sense returned! Absolute time, a "cosmological" time since the big bang, when the universe is thought to have begun to expand, can be defined theoretically. It is assumed (this not being contradicted by observation), that the distribution of matter in the universe, when "averaged" over very large distances, is uniform, having a constant density at a given time -- time being defined as what is measured by clocks moving with the mean distribution of matter -- and will flow "on average" at the same rate everywhere. As the universe expands, the mean density will decrease while the absolute time increases.

What is thought by most specialists to be absolute motion can be measured from observations. It is believed to be the motion relative to weak diffuse electromagnetic radiation observed to be coming from all directions in the sky. It is invisible to the eye, its wavelengths being much larger than those of visible light. This radiation is thought to be a remnant of radiation emitted everywhere when the universe, which was then much hotter than now, was becoming transparent some time after the big bang (see section 5 of the last chapter).

The subsequent continuing expansion of the Universe would then have considerably increased the wavelength of the radiation. Almost equal amounts of this radiation come from all directions, this property being called "isotropy". The first deviation from isotropy is usually explained by specialists as due to the motion of the observer relative to the radiation, though this interpretation is not 100 per cent certain. Because of an effect in physics called the Doppler effect, motion towards a source of waves decreases their wavelength; motion moving away from the source increases the wavelength. An absolute motion of the solar system very close to 370km/sec. has been measured from observations of this radiation using the COBE satellite.

A number of misconceptions have arisen concerning relativity. This is perhaps because in a certain way the Minkowski space-time of special relativity and the curved space-time of general relativity have replaced Newton's absolute space and universal time. Time, or more precisely its space-like aspects, has become a kind of space, being indeed indistinguishable from the latter. In this way the study only of the space-like aspects of time has led to a sort of logical conclusion, the fusion of space and time. According to this way of thinking, the world line of a particle appears to be eternal, as it is independent of time. In part of a radio programme I heard about science and religion, it was even claimed, from what I remember, that this was evidence for the existence of God.... In fact each observer will experience time in his or her own way, this being different from that of other observers. The time of a distant event, which could be due to an action of a living organism (or, as we shall see according to the ideas developed later in this book, an act of its willing), will appear for a particular observer to be the time when a result of such an act is perceived, or a signal is received from the distant event. If the observer is human he or she will still experience time, as described in the last chapter. The actions of other living organisms perceived at a certain time can still influence what happens at later times, but cannot influence previous events perceived by the observer, as relativity does not contradict the ordinary ideas of cause and effect. Relativity, unlike the other twentieth century developments now to be discussed,does not involve the unpredictable. Indeed Einstein resisted the apparent reality of the discovery of the unpredictable in quantum physics. His statement that "God does not play with dice" is very well known.

While relativity introduces a fundamental change in ideas about space and time without considering the unpredictable, I shall now describe phenomena which involve the unpredictable, without radically changing the ideas about space and time. In fact, the unpredictable is even hidden in Newton's laws! In many situations, which can be very simple, motion is extremely sensitive to minute unmeasurable perturbations. Thus in practice prediction becomes impossible, even when the future is determined by Newton's laws. Such situations are now called "chaos", following James Yorke, who wrote a paper on it in 1975 with Tien-Yien Lee, a student. A popular readable account of chaos is given in the book "Chaos: making a new science" by the scientific journalist James Gleick (Cardinal, Sphere books 1988). It is because of the phenomenon of chaos that the idea of a completely predictable universe based on Newton's laws, which was stated very clearly by the French mathematician Pierre Simon de Laplace (1749-1827), is now known to have been quite wrong.

This form of the unpredictable is already apparent in the calculations made by the great French mathematician Henri Poincarè (1854-1906) shortly before 1900 based on classical mechanics. Not much notice was taken of it until the 1961 computer calculations of the American meteorologist Edward Lorenz, using an extremely simple mathematical model, first showed that even a highly unrealistic model of the weather cannot lead to predictions a very long time in advance. First results were published in 1963. He found that unpredictability could even occur when motion was described by only 3 equations. Other researchers, who did not always know about the work of others in the field, made independent contributions. For instance F. Ruelle and F. Takens came to a similar conclusion to that of Lorenz from the study of turbulence in a fluid in an article published in 1971. Chaos was also found to be important in the mathematical description of the variation with time of the number of living organisms of a particular kind belonging to a certain population. Chaotic processes in different situations, such as those of certain chemical reactions, were described in a book written in French by Ilya Prigogine and Isabelle Stengers, "La Nouvelle Alliance" (Gallimard 1979), without the authors apparently being aware of much of the work already done by other people on chaos theory. It may be noted that previous work done in the Soviet Union is also relevant to this theory.

It is also interesting to note that two of the fathers of chaos theory, Mitchell Feigenbaum and Albert Libchaber, were interested in the scientific ideas of Goethe, mentioned in the previous chapter. This is perhaps indicative of the radical nature of the change in ideas brought about by this theory.

In order to understand a little what is involved, let us look at the paths of particles, obeying Newton's laws, on which different forces act. A very useful concept in this respect is that of "phase space". This is a completely abstract space, which in the framework of these laws has the 3 dimensions of ordinary space and three dimensions of momentum (mass times velocity in each of the 3 directions) for each independently moving particle belonging to a system of particles which is studied. This means that each particle has 6 dimensions in phase space. So if there are n particles in the system, phase space will have 6n dimensions. It should be noted that if all particles are not independent and/or they are not free to move in all directions, all 6n dimensions need not be taken into account. Now there is a mathematical theorem for particles moving in phase space called the Liouville theorem, which leads to the conclusion that if one studies different possible systems of the same number n particles, with each having a different set of trajectories, the volume of phase space occupied by the different systems does not change with time. What must be emphasized is that the shape of a constant volume is not fixed, it could be the 6n dimensional equivalent of a sphere or, on the contrary, a very long and narrow spaghetti-like region in 6n dimensions, having the same volume. When a chaotic situation occurs, a group of systems of particles at first occupying a small sphere-like volume in phase space and so having both positions and speeds which are almost the same, will later occupy such an extremely thin spaghetti-like volume. The spigot-like volume becomes almost "infinitely" thin and is folded a very large "almost infinite" number of times. In this way, corresponding particles belonging to two such systems can become widely separated in space and also have quite different speeds. The volume in phase space which the systems tend to occupy as time passes, will have a "strange" structure, which is called a "strange attractor".

There is a special geometry which describes such a situation associated with the presence of chaos. It is the geometry of fractals, the expression "fractal" having been invented by the mathematician Benoit Mandelbrot. A fractal object will have structure on all scales down to the infinitely small, the same structure being repeated on different scales. The construction of fig. 3.1 shows a very simple example of how to make a fractal figure in the two dimensions of the surface of the page. We start with an equilateral triangle, each of whose sides are divided into three equal parts. Then two sides of a new equilateral triangle pointing outwards are constructed on the central third of each line of the original triangle, this central part being removed. Each side of the figure then obtained is again divided into three equal parts; a new equilateral triangle being erected on the central part, which is then removed. The process is repeated an infinitely large number of times for each side of the figure. In this way an infinitely long figure with structures on infinitely small scales is obtained, but which still fits onto the page! 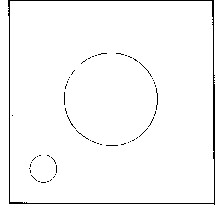By this process we obtain a "fractal snowflake".

Another basic concept connected with chaos is the time scale over which a system becomes chaotic, called the Lyapunov time. The distance between two particle paths which start to diverge from each other in phase space is given by what is called an exponential law. After a short time t, the distance between the paths for two particles which were originally very close becomes equal to Ae^{(t/l )}, where A is a constant, e is a very famous number near 2.718 and l is the Lyapunov time. For times which are much longer than the Lyapunov time, the two paths are very widely separated and the behavior of the system becomes most sensitive to its initial conditions and therefore unpredictable. Thus the system can be said to have lost its "memory" of what were the initial conditions.

The sensitivity of chaotic systems to their initial conditions and to small perturbations can be dramatic and is sometimes called the "butterfly effect". The idea is that the flapping of the wing of a butterfly can completely change the weather at a later date; a distant storm could be produced. The idea is not quite correct, however, as it is impossible to relate the flapping of a particular wing to the production of any particular effect such as a storm. All small and/or distant perturbations have large effects; there is, in fact, a kind of abyss between causes and effects.

It must be emphasized that chaos can occur in extremely simple situations. Fig 3.2 shows what is called Sinai billiards. In the figure there is a billiard table with a flat frictionless surface and a square outer boundary. There is a central obstacle on the table. A billiard ball is then supposed to be able to bounce between the sides and the obstacle. Under these conditions the path of the billiard ball is chaotic.

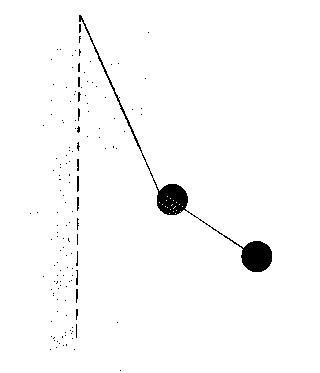
Chaotic behavior can be shown in a another situation by a double pendulum without friction (fig 3.3). A second pendulum is suspended from a first one. Four types of motion can occur: stationary; periodic, when the ratio of the periods of oscillation of each pendulum is a ratio of two whole numbers; "quasi periodic", when the ratio of the periods is an irrational number, that is, a number which is not equal to any fraction. Examples of irrational numbers are the square roots of 2, 3 and 5 and the number p And, finally, the motion can be chaotic.

Astronomical phenomena were thought at one time to be particularly good examples of predictable situations. However, chaos is even present in the motions of the bodies of the solar system. The most striking example is that of one of Saturn's satellites, Hyperion. Its shape is far from that of a sphere, its length being about twice its width. The axis and speed of rotation of Hyperion vary in an unpredictable way over a time scale of a few orbital periods (one period is 21 days!). Haley's comet has been fairly periodic for two millennia; however, observations of the comet before the second century BC would be difficult to explain from calculations based on what is known about its present orbit. In fact, the motion of Haley's comet is partly chaotic. Phenomena of chaos also have a strong influence on the properties of the orbits of certain asteroids -- the asteroids being very small planets whose orbits mainly lie between those of Mars and Jupiter.

Chaos is also present in the motions of larger planets over very long time scales. The prediction of the motion of Pluto has been shown to be impossible for times of more than about 400 million years. Similarly, predictions of the motions of the inner planets (Mercury, Venus, Earth and Mars) will be completely different than their real behavior more than 100 million years later. According to calculations by Jacques Laskar published in 1994, chaotic effects over a time scale of less than three thousand five hundred million years could even lead to the ejection of Mercury from the solar system, following a close approach to Venus! We might wonder whether ejection of other small planets such as one inside the orbit of Mercury have already occurred. These studies, however, indicate that the orbits of the most massive planets -- Jupiter, Saturn, Uranus and Neptune -- are virtually unaffected by chaotic phenomena.

There are indications that chaos plays a fundamental role in living organisms, though much remains to be elucidated in this field. As already mentioned, the populations of living creatures of a certain type can vary with time in a chaotic way. A. L. Goldberger And B. J. West suggested in 1987 that the normal functioning of the heart is chaotic -- in which case an excessively regular behavior of a person's heart would be extremely serious for his or her health. This idea was expounded in a more popular way by A. L. Goldberger, D.R. Rigney and B.J. West in an article "Chaos and Fractals in Human Physiology" (Scientific American, vol. 262, no. 2, p. 34, 1990). In the same way the functioning of the nervous system in general and the brain in particular show signs of the presence of chaos, which may be essential for what they normally do, such as reacting to sense impressions (see "The Physiology of Perception" by W.J. Freeman in the Scientific American, vol. 264, no. 2, p.34 1991). Let us note, however, that it is not easy to prove in a mathematically rigorous way that chaos is present. On the other hand, it is at least reasonable to think that many processes inside the body of a living organism satisfy the mathematical conditions for chaos.

Another way of looking at life would be to consider it to be the frontier between predictability and chaos. S.A. Kauffman in "Antichaos and Adaptation" (Scientific American, vol. 265, no.2, p. 64 1991) describes mathematical models called Boolean networks, considered by the author to represent the action of genes in living organisms. These models are used to describe how different sorts of cell in the body of a living organism first appear and how evolution proceeds according to Darwin's natural selection. The author mentions different behaviors of such a model, including even a sort of chaotic behavior, when the future development of a model is extremely sensitive to its exact state at a particular time. The author refers to what for many may seems a surprising comparison with the states of matter, suggested by the computer scientist Christopher Langton. According to him predictability is like the solid state and chaos like the gaseous state. The processes of life in such a framework are similar to the intermediate liquid state. This is surprising when it is remembered that in a number of esoteric traditions living organisms are considered to have what are called "etheric bodies", while Rudolf Steiner relates the nature of the etheric to that of water, which is the liquid most commonly encountered by human beings in ordinary daily life. However, it should be noted that the validity of Langton's own calculations has been challenged. We can see in any case that even though the application of the models mentioned may appear to be extremely schematic and materialistic, striking conclusions can be drawn from them, which contain very interesting lessons for us. In particular the idea of life as being between the predictable and unpredictable agrees with normal human intuition; heredity for example, like many other aspects of living organisms, is thought of as being at least partly predictable.

We can conclude from this discussion of chaos that physical systems obeying mathematical laws can become extremely sensitive to infinitesimal, almost "non-physical" perturbations from the outside. Such systems are in a way "vessels" able to receive what cannot be grasped in the framework of physical predictability, that is, effects which one might think of as being "outside physics". It must be emphasized that as a result of the already mentioned abyss between causes and effects, it is not possible for anybody to physically act on such systems to produce a desired result, unless the systems are continually perturbed over time scales of the order of not much more than the Lyapunov time. This can be understood as being due to the unpredictable effects over longer time scales of any single perturbation at a given time. Living organisms may be good examples of chaotic systems which persist over a long time or perhaps of systems on the border between chaos and predictability. In this way the old arguments about whether or not living organisms possess something not possessed by the non-living, or obey different laws, or, in the language of esoteric traditions, the nature of the "etheric" may in principle be resolvable. Various conceivable implications of such results will be discussed later in this book.